ตรรกศาสตร์คืออะไร
“ตรรกศาสตร์” คือระบบวิชาความรู้ที่เกี่ยวข้องกับความคิดและการให้เหตุผล ใช้เป็นเครื่องมือในการเข้าถึงหลักปรัชญาต่างๆ และเป็นพื้นฐานในหลายๆสาขาวิชา และสำหรับวิชาคณิตศาสตร์ น้องๆจะได้เรียนตรรกศาสตร์ในเป็นรูปแบบและกฎเกณฑ์ีการให้เหตุผลทางคณิตศาสตร์ (Mathematical Logic) ไม่ว่าจะเป็น “และ” “หรือ” “ถ้า..แล้ว” “ก็ต่อเมื่อ” และนิเสธ นอกจากนี้ หลักตรรกศาสตร์จะใช้สำหรับการพิสูจน์ทฤษฎีต่างๆ และนำไปใช้ต่อยอดในการเขียนโปรแกรมคอมพิวเตอร์ สร้างเป็นพีชคณิตในทางดิจิตอล ฯลฯ
ในวิชาคณิตศาสตร์ เราจะได้เริ่มทำความรู้จักกับ “ตรรกศาสตร์” ในชั้นม. 4 ตั้งแต่เทอมแรกกันเลย เนื้อหาที่เรียนจะเกี่ยวกับประพจน์ การเชื่อมประพจน์ รวมไปถึงการหาค่าความจริงของประพจน์ สมมูลและนิเสธของประพจน์ สัจนิรันดร์และการอ้างเหตุผล สุดท้ายเราจะได้เรียนเรื่องตัวบ่งปริมาณและประโยคเปิดว่ามีรูปแบบและลักษณะเป็นอย่างไรด้วย
ประพจน์
“ประพจน์” คือ ประโยคหรือข้อความบอกเล่าหรือปฏิเสธที่มีค่าความจริง เป็นจริงหรือเท็จ อย่างใดอย่างหนึ่งเท่านั้น
- ข้อความที่อยู่ในรูปของคำสั่ง คำขอร้อง คำอุทาน คำอ้อนวอน คำแสดงความปรารถนา
สุภาษิตคำพังเพย ประโยคเปิดเป็นข้อความที่ไม่เป็นประพจน์ - ประโยคที่มีความจริงไม่แน่นอน ไม่สามารถระบุว่าเป็นจริงหรือเท็จได้ ไม่เป็นประพจน์
- ข้อความบอกเล่าที่มีตัวแปรอยู่ด้วย ไม่สามารถบอกว่าจริงหรือเท็จจะไม่เป็นประพจน์
เราเรียกมันว่า “ประโยคเปิด”
ตัวอย่างประโยคที่เป็นประพจน์
ดาวเสาร์เป็นดาวเคราะห์ (จริง)
เขื่อนลำตะคองไม่ได้อยู่ในจังหวัดกรุงเทพฯ (จริง)
8 ไม่เท่ากับ 3 (จริง)
15 – 8 > 20 (เท็จ)
2 เป็นจำนวนตรรกยะ (เท็จ) ( รอใส่ root )
ตัวอย่างประโยคที่ไม่เป็นประพจน์
100 บวก 20 มีค่าเท่าไหร่ (ประโยคคำถาม)
จงเขียนประโยคบอกเล่า (ประโยคคำสั่ง)
โปรดอย่าเดินลัดสนาม (ข้อความขอร้อง)
ให้อภัยฉันด้วยเถิด (ข้อความอ้อนวอน)
อยากกินเค้กอร่อยๆ (ข้อความแสดงความปรารถนา)
ว้าว สวยจัง (คำอุทาน)
ไก่ได้พลอย (สุภาษิตคำพังเพย)
เธอเป็นนักกีฬา (ประโยคเปิด)
เรานิยมใช้สัญลักษณ์ p, q, r, s หรือตัวอักษรภาษาอังกฤษอื่นๆ แทนประพจน์
การแจกแจงความจริงของประพจน์
ประพจน์ที่มีค่าความจริงเป็นจริง ใช้สัญลักษณ์ T
ประพจน์ที่มีค่าความจริงเป็นเท็จ ใช้สัญลักษณ์ F
ถ้าโจทย์ไม่ได้กำหนดค่าความจริงของประพจน์ย่อยๆมาให้ เราต้องแจกแจงค่าความจริงที่อาจจะเกิดขึ้นได้ทั้งหมดจากประพจน์ย่อยๆ นั้น เราเรียกวิธีนี้ว่า “การแจกแจงความจริง” หรือ “การหาค่าความจริงของประพจน์” ซึ่งวิธีที่นิยมในมากที่สุดคือ การสร้างตารางค่าความจริง
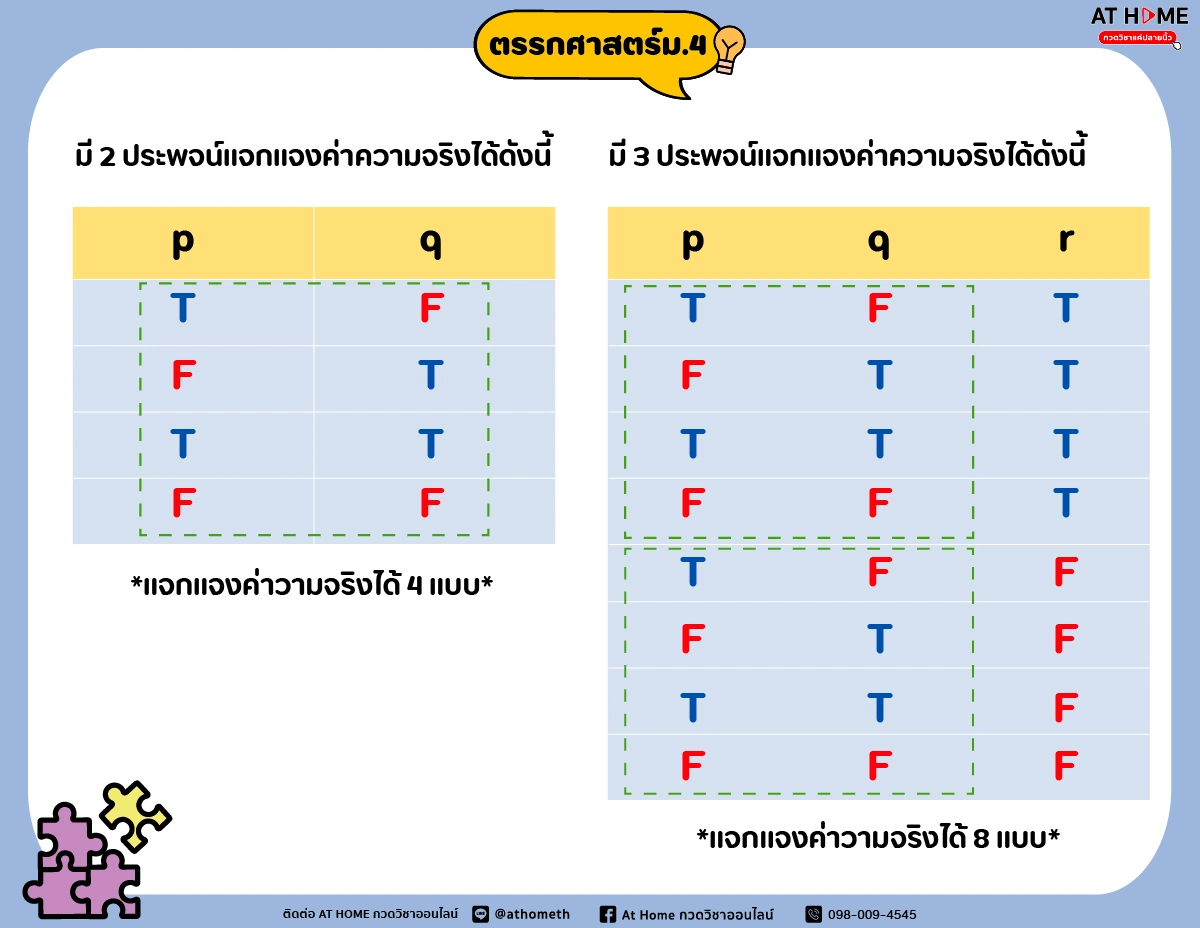
เราสามารถหาจำนวนวิธีแจกแจงได้โดยใช้สูตร
จำนวนวิธีแจกแจง = 2n
โดยให้ n คือจำนวนของประพจน์
เช่น ถ้ามีประพจน์ 5 ประพจน์ จะเขียนแจกแจงความจริงได้ 25 = 32 แบบ
การเชื่อมประพจน์
ถ้าให้ p และ q เป็นประพจน์ เมื่อนำประพจน์มาเชื่อมกันด้วยตัวเชื่อมแล้ว เราจะเรียกประพจน์ใหม่นี้ว่า “ประพจน์เชิงประกอบ” ซึ่งตัวเชื่อมที่ใช้จะมี 5 ตัว ได้แก่
| ตัวเชื่อม “และ” ใช้สัญลักษณ์ คือ ” ∧ “ ตัวเชื่อม “หรือ” ใช้สัญลักษณ์ คือ ” ∨ “ ตัวเชื่อม “ถ้า… แล้ว…” ใช้สัญลักษณ์ คือ ” → “ ตัวเชื่อม “ก็ต่อเมื่อ” ใช้สัญลักษณ์ คือ ” ↔ “ ตัวเชื่อม “นิเสธ” ใช้สัญลักษณ์แทนด้วย ” ~ “ |
ตารางค่าความจริงของตัวเชื่อมแบบต่างๆ
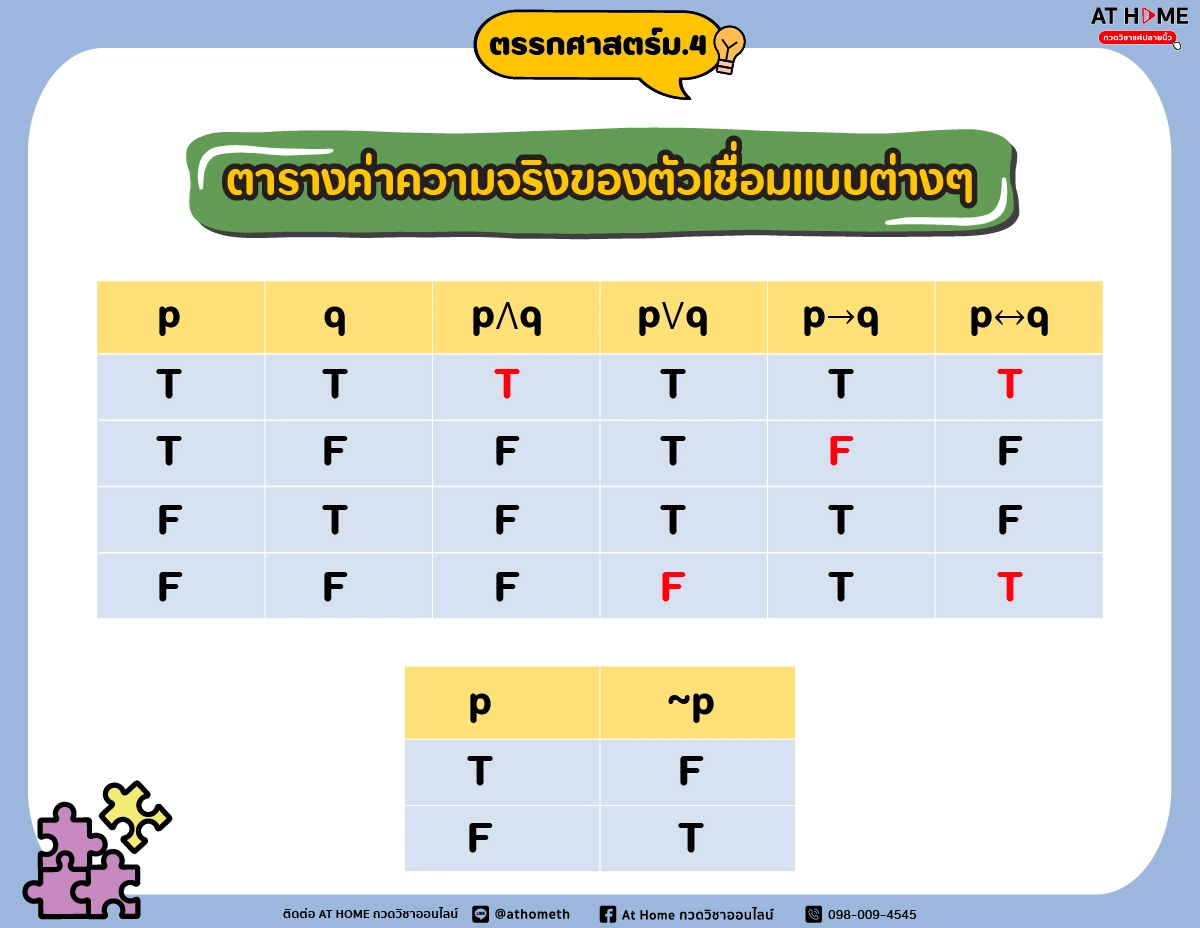
จากตารางสามารถสรุปได้ดังต่อไปนี้
- ตัวเชื่อม “และ” (∧) เป็นจริงเพียงกรณีเดียวคือ T∧T เป็น T
- ตัวเชื่อม “หรือ” (∨) เป็นเท็จเพียงกรณีเดียวคือ F∨F เป็น F
- ตัวเชื่อม “ถ้า…แล้ว…” (→) เป็นเท็จเพียงกรณีเดียว คือ T → F เป็น F
- ตัวเชื่อม “ก็ต่อเมื่อ” (↔) ถ้ามีค่าความจริงเหมือนกันจะเป็นจริง ไม่เหมือนกันจะเป็นเท็จ
- นิเสธของประพจน์ คือ ประพจน์ที่มีค่าความจริงตรงกันข้ามกับประพจน์นั้นๆ จากจริงเป็นเท็จ จากเท็จเป็นจริง
ข้อควรระวังในการหาค่าความจริงของประพจน์
- ถ้ามีวงเล็บ ให้หาความจริงในวงเล็บก่อน
- ถ้าไม่มีวงเล็บ ให้หาความจริงของ “~” ก่อน แล้วจึง “∧” “∨” “→” และ “↔” ตามลำดับ
ตัวอย่าง จงสร้างตารางค่าความจริงทุกกรณีที่เป็นไปได้ของประพจน์ p → (q ∧ s)
วิธีทำ ประพจน์ p → (q ∧ s) มีประพจน์ย่อย คือ p, q และ s
ดังนั้นจำนวนวิธีที่แจกแจงได้ทั้งหมด คือ 23 = 8 แบบ และสร้างตารางได้ดังนี้
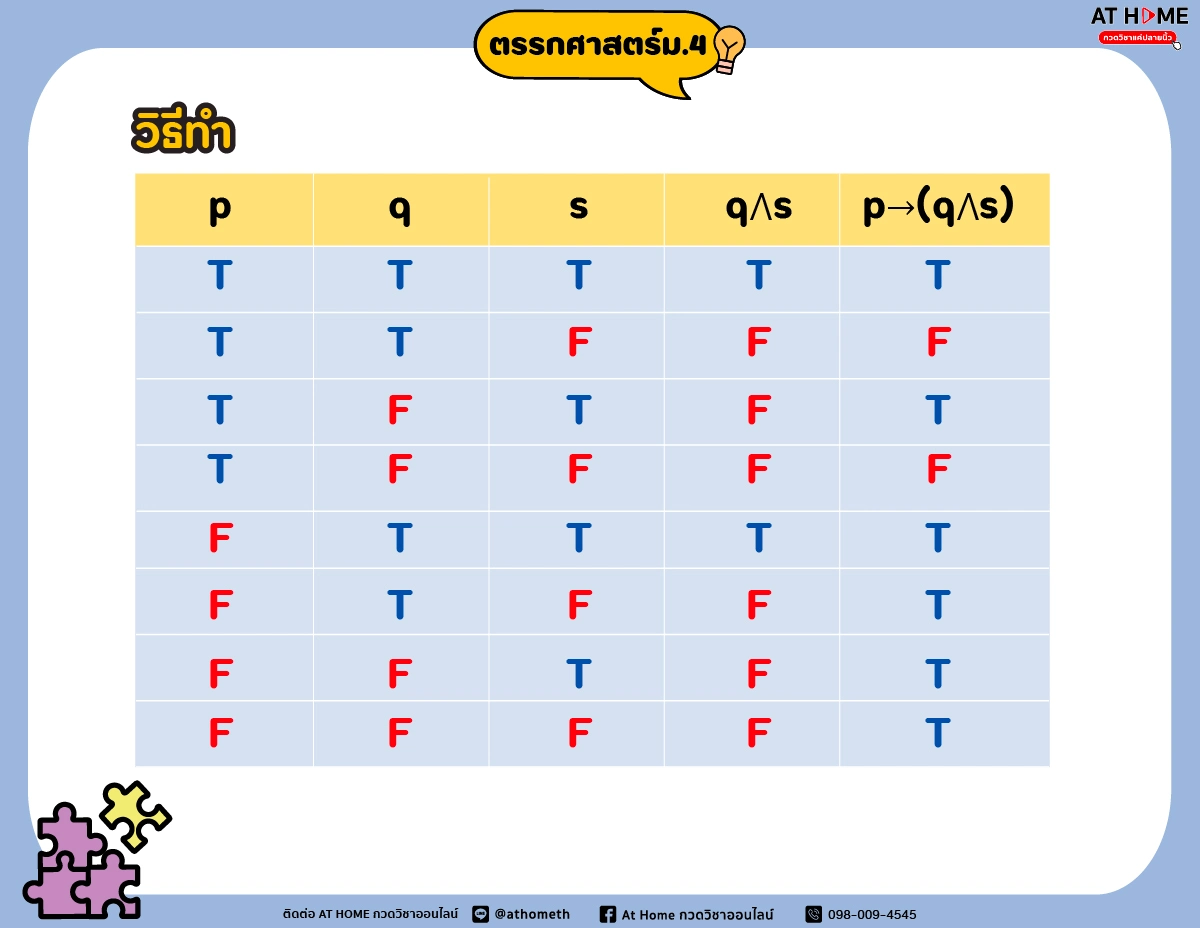
เทคนิคการสร้างตารางแจกแจงความจริง
- หาจำนวนวิธีแจกแจงโดยใช้สูตร 2n
- เริ่มจากเขียนประพจน์ตัวแรก เขียน T ลงมาครึ่งหนึ่ง และเขียน F อีกครั้งที่เหลือ
- จำนวนค่าความจริงของประพจน์ตัวต่อไป ก็จะเป็นครึ่งหนึ่งของประพจน์ตัวก่อน
ประพจน์ที่สมมูลกัน
ประพจน์สองรูปแบบจะสมมูลกันได้ ก็ต่อเมื่อ ประพจน์ทั้งสองมีค่าความจริงเหมือนกันทุกกรณี
และสามารถนำไปใช้แทนกันได้ โดยใช้สัญลักษณ์ “ ≡ ” แทนคำว่าสมมูล
การตรวจสอบว่าประพจน์สมมูลกันหรือไม่ สามารถทำได้ 2 วิธี คือ
การใช้ตารางแจกแจงความจริง หรือ การใช้สมบัติสมมูลของประพจน์
สมบัติการสมมูล
มีรูปแบบของประพจน์ที่สมมูลกันหลายรูปแบบ ดังต่อไปนี้
- สมบัติการสลับที่
p ∧ q ≡ q ∧ p
p ∨ q ≡ q ∨ p
p ↔ q ≡ q ↔ p
- สมบัติการเปลี่ยนกลุ่ม
p ∧ ( q ∧ r ) ≡ ( p ∧ q ) ∧ r ≡ p ∧ q ∧ r
p ∨ ( q ∨ r ) ≡ ( p ∨ q ) ∨ r ≡ p ∨ q ∨ r
p ↔ ( q ↔ r ) ≡ ( p ↔ q ) ↔ r ≡ p ↔ q ↔ r
- สมบัติการแจกแจง
p ∧ ( q ∨ r ) ≡ ( p ∧ q ) ∨ ( p ∧ r )
p ∨ ( q ∧ r ) ≡ ( p ∨ q ) ∧ ( p ∨ r )
p → ( q ∨ r ) ≡ ( p → q ) ∨ ( p → r )
p → ( q ∧ r ) ≡ ( p → q ) ∧ ( p → r )
( p ∨ q ) → r ≡ ( p → r ) ∧ ( p → r )
( p ∧ q ) → r ≡ ( p → r ) ∨ ( p → r )
- สมบัติของ “ถ้า..แล้ว..” ( → )
p → q ≡ ~q → ~p ≡ ~p ∨ q
- สมบัติของ “ก็ต่อเมื่อ” ( ↔ )
p ↔ q ≡ ( p → q ) ∧ (q → p )
- สมบัติของนิเสธ ( ~ )
~(~p) ≡ p
~(p ∧ q) ≡ ~p ∨ ~q
~(p ∨ q) ≡ ~p ∧ ~q
~(p → q) ≡ p ∧ ~q
~(p ↔ q) ≡ ~p ↔ q ≡ p ↔ ~q
- สมบัติอื่นๆ
p ∧ p ≡ p
p ∧ T ≡ p
p ∧ F ≡ F
p ∧ ~p ≡ F
p ∨ p ≡ p
p ∨ T ≡ T
p ∨ F ≡ p
p ∨ ~p ≡ T
p → F ≡ ~p
F → p ≡ T
p → T ≡ T
T → P ≡ P
P ↔ P ≡ T
P ↔ ∼P ≡ F

สัจนิรันดร์
“สัจนิรันดร์” คือ ประพจน์ที่มีค่าความจริงเป็นจริงทุกกรณี มีวิธีการตรวจสอบ 3 วิธี ได้แก่
- สร้างตารางค่าความจริง เพื่อหาค่าความจริงทุกรูปแบบที่เป็นไปได้ ถ้าความจริงขั้นสุดท้ายของประพจน์เป็นจริงทุกกรณี แสดงว่าประพจน์นั้นเป็นสัจนิรันดร์
- ใช้วิธีหาข้อขัดแย้ง ซึ่งวิธีนี้นิยมใช้กับตัวเชื่อม “หรือ” กับ “ถ้า..แล้ว..” หากใช้กับ “และ” , “ก็ต่อเมื่อ” อาจจะต้องทำหลายครั้ง มีวิธีการคือ สมมติให้ประพจน์มีค่าความจริงเป็นเท็จ แล้วจากนั้นก็ย้อนกลับไปดูประพจน์ย่อยๆ ว่าขัดแย้งกันหรือไม่ ถ้าขัดแย้งกัน แสดงว่าไม่มีโอกาสเป็นเท็จ ประพจน์นั้นจะเป็นสัจจนิรันดร์
- การใช้หลักสมมูล เราจะใช้วิธีนี้กับตัวเชื่อม “ก็ต่อเมื่อ” โดยมีหลักการ Δ ↔ Ο ถ้า Δ ≡ Ο จะได้ว่า Δ ↔ Ο เป็นสัจจนิรันดร์
การอ้างเหตุผล
“การอ้างเหตุผล” คือ การตรวจสอบว่าข้อความที่กำหนดให้ชุดหนึ่ง แล้วทำให้เกิดข้อความอีกชุดนั้น สมเหตุสมผลหรือไม่ หรือ การหาผลสรุปจากเหตุที่กำหนดให้นั่นเอง
การอ้างเหตุผล ประกอบด้วย
- เหตุ คือ ส่ิงที่ถูกกำหนดมาให้ ประกอบด้วยประพจน์ย่อยๆ P1, P2, P3…,Pn
- ผล คือ ผลสรุปจากเหตุ แทนด้วย Q
1. นำเหตุมาเชื่อมกันด้วย ∧ และนำ → มาเชื่อมกับผล หลังจากนั้นให้ตรวจว่าเป็นสัจนิรันดร์
(P1∧P2∧P3∧…∧Pn) → Q
หากเป็นสัจนิรันดร์แสดงว่าการอ้างเหตุผลนี้ สมเหตุสมผล (Valid)
หาไม่เป็นสัจนิรันดร์แสดงว่าการอ้างเหตุผลนี้ ไม่สมเหตุสมผล (Invalid)
2. ให้เหตุทุกข้อเป็นจริง (T) หาค่าความจริงและไปแทนในผล
ถ้าผล เป็นจริง (T) แสดงว่า สมเหตุสมผล
ถ้าผล เป็นเท็จ (F) แสดงว่า ไม่สมเหตุสมผล
3. ใช้รูปแบบที่มีการพิสูจน์แล้วว่าสมเหตุสมผล
ประโยคเปิด
“ประโยคเปิด” คือ ประโยคบอกเล่าหรือประโยคปฏิเสธที่มีตัวแปร เมื่อแทนค่าตัวแปรด้วยสมาชิกในเอกภพสัมพัทธ์แล้วประโยคเปิดนั้นจะเป็นประพจน์ เช่น
“เธอใส่เสื้อสีเขียว” เป็นประโยคเปิด เพราะมีคำว่า “เธอ” เป็นตัวแปร ไม่ระบุว่าใคร หากเปลี่ยนเป็น “มาลีใส่เสื้อสีเขียว” ประโยคนี้จะเป็นประพจน์เพราะระบุตัวแปรเรียบร้อยแล้ว
“a เป็นจำนวนคู่” เป็นประโยคปเปิด เพราะมีตัวแปร “a” ถ้าแทนค่า a = 8 ประโยคจะเปลี่ยนเป็น “8 เป็นจำนวนคู่” ประโยคนี้จึงกลายเป็นประพจน์
ตัวบ่งปริมาณ
“ตัวบ่งปริมาณ” คือ ข้อความที่บอกจำนวนของตัวแปรในประโยคเปิดว่ามีมากน้อยแค่ไหน มี 2 ประเภท คือ
- ∀x หมายถึง x ทุกตัวที่อยู่ในเอกภพสัมพัทธ์
เช่น สำหรับ x ทุกตัวซึ่ง x+5=4 เขียนแทนด้วย ∀x[x+5=4]
- ∃x หมายถึง x บางตัวที่อยู่ในเอกภพสัมพัทธ์
เช่น มี x อย่างน้อยหนึ่งตัว ซึ่ง 2x-3 < -1 เขียนแทนด้วย ∃x[2x-3 < -1]
เนื้อหา “ตรรกศาสตร์” ในชั้นม.4 เทอม 1 ที่น้องๆจะต้องเรียนก็มีประมาณนี้ อาจจะต้องใช้เวลาในการทำเข้าใจอยู่บ้าง แต่พี่เชื่อว่าไม่น่าจะยากเกินไปถ้าเราขยันและตั้งใจ หรือถ้าน้องคนไหนยังรู้สึกว่าอ่านยังไงก็ยังไม่เข้าใจ ยังอยากได้คอร์สเรียนเพื่อปูพื้นฐานให้แน่นขึ้น หรือจะเป็นคอร์สเรียนตรรกะศาสตร์แบบตะลุยโจทย์ไปพร้อมกัน ทาง At Home ก็คัดสรรคอร์สเรียนมากมายมาให้เลือก แอบกระซิบว่ามีคอร์สเรียนฟรีด้วยนะ ไปลุยกันได้เลย

FAQ ตัวอย่างข้อสอบ “ตรรกศาสตร์”พร้อมเฉลย
จงตรวจสอบว่าประพจน์ต่อไปนี้สมมูลกันหรือไม่ ∼[(p∧q)→(∼q∨r)] กับ p∧∼(q→r)
วิธีทำ
∼[(p∧q)→(∼q∨r)] ≡ ∼[∼(p∧q)∨(∼q∨r)] ใช้สมบัติของ ถ้า..แล้ว..
≡ (p∧q)∧∼(∼q∨r) ใช้สมบัติของนิเสธ
≡ (p∧q)∧(q∧∼r) ใช้สมบัติของนิเสธ
≡ p∧q∧q∧∼r ตัวเชื่อมเหมือนกันถอดวงเล็บออกได้เลย
≡ p∧(q∧q)∧∼r ใช้สมบัติเปลี่ยนกลุ่ม
≡ p∧q∧∼r ใช้สมบัติ p ∧ p ≡ p
≡ p∧∼(q→r) ใช้สมบัติ~(p→q) ≡ p∧~q
ตอบ ดังนั้นประพจน์ ∼[(p∧q)→(∼q∨r)] กับ p∧∼(q→r) สมมูลกัน
จงตรวจสอบว่าประพจน์ (p∧q)→(p∨q)(p∧q)→(p∨q) เป็นสัจนิรันดร์หรือไม่
วิธีทำ สร้างตารางค่าความจริงเพื่อตรวจสอบความเป็นสัจนิรันดร์ได้ตารางดังนี้ 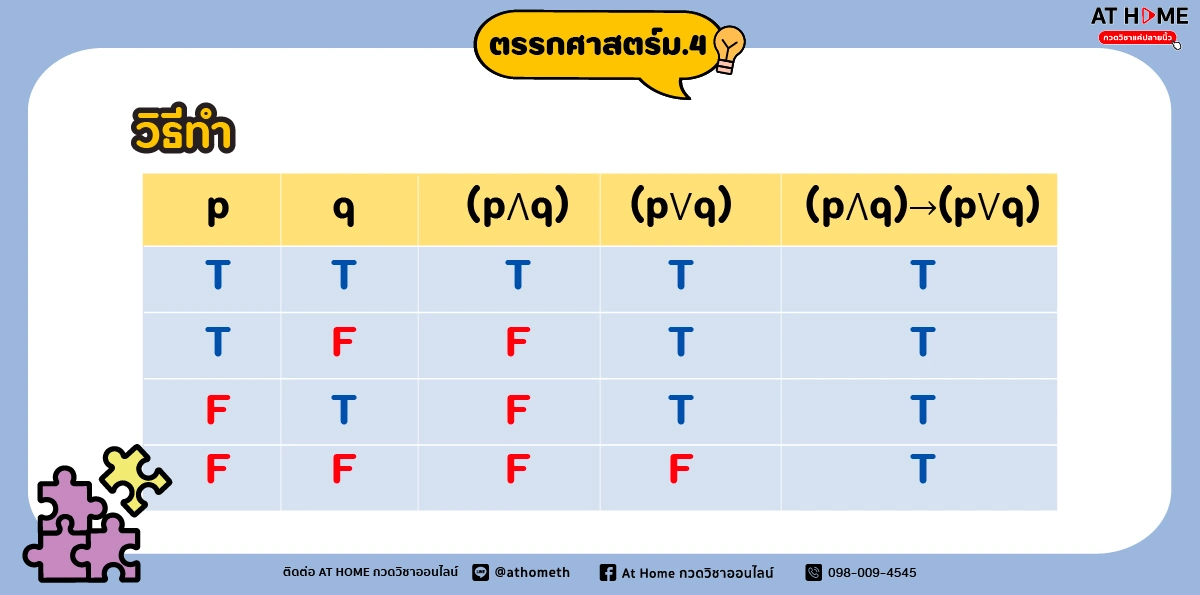
ตอบ จากตารางค่าความจริงที่สร้างขึ้น พบว่าทุกกรณีที่เป็นไปได้นั้นมีค่าความจริงเป็นจริงทั้งหมด ดังนั้นประพจน์ที่กำหนดให้จึงเป็นสัจนิรันดร์
ประโยคต่อไปนี้ประโยคใดบ้างเป็นประพจน์
-เดือนมีนาคมนี้น้ำท่วมกรุงเทพหรือไม่
-อย่าลอกคำตอบเพื่อน
-ดาวฤกษ์ไม่มีแสงสว่างในตัวเอง
-x + 5 = 36
ข้อ 3. เป็นประพจน์ เพราะเป็นประโยคปฏิเสธที่มีค่าความจริงเป็นเท็จ
ข้อ 1 ไม่เป็นประพจน์ เพราะเป็นประโยคคำถาม
ข้อ 2 ไม่เป็นประพจน์ เพราะเป็นประโยคคำสั่ง
ข้อ 4 ไม่เป็นประพจน์ เพราะมีตัวแปร x





