สรุป จำนวนเชิงซ้อน พร้อมแบบฝึกหัดและเฉลยแบบละเอียด

“จำนวนเชิงซ้อน” เลขม.ปลาย นั้นเป็นบทที่สำคัญมาก ๆ และเหมาะที่จะเก็บคะแนนสำหรับน้อง ๆ ที่เตรียมตัวสอบเข้ามหาวิทยาลัยหรือกำลังตั้งใจเก็บเกรดในโรงเรียน พี่ ๆ ATHOME ได้สรุปย่อแบบเข้าใจง่ายพร้อมนิยามต่าง ๆ ที่ต้องรู้ให้อย่างครบถ้วน

จำนวนเชิงซ้อน

จำนวนเชิงซ้อน

---

บทนิยาม

สำหรับจำนวนเชิงซ้อน z = a + bi เมื่อ a,b เป็นจำนวนจริง

เรียก a ว่า ส่วนจริง ของ z เขียนแทนด้วย Re(z)

และเรียก b ว่า ส่วนจินตภาพ ของ z เขียนแทนด้วย Im(z)

ถ้า Im(z) = 0 แล้ว z เป็นจำนวนจริง

ถ้า Re(z) = 0 และ Im(z) ไม่เท่ากับ 0 แล้ว z จะเป็นจำนวนจินตภาพแท้

---

บทนิยาม

ให้ z = a + bi    = (a,b)  ,a , b R , i² = -1

และ w  = c + di   = (c,d) , c , d R ( รอเปลี่ยนเครื่องหมายสมาชิก )

1. การเท่ากัน 
   z = w ก็ต่อเมื่อ a = c และ b = d
   

1. การบวก
   z + w = (a+c) + (b+d)i
   = (a+c, b+d)
   

3. การคูณ  
   zw = (ac – bd) + (ad + bc)i
   = (ac – bd, ad + bc)

---

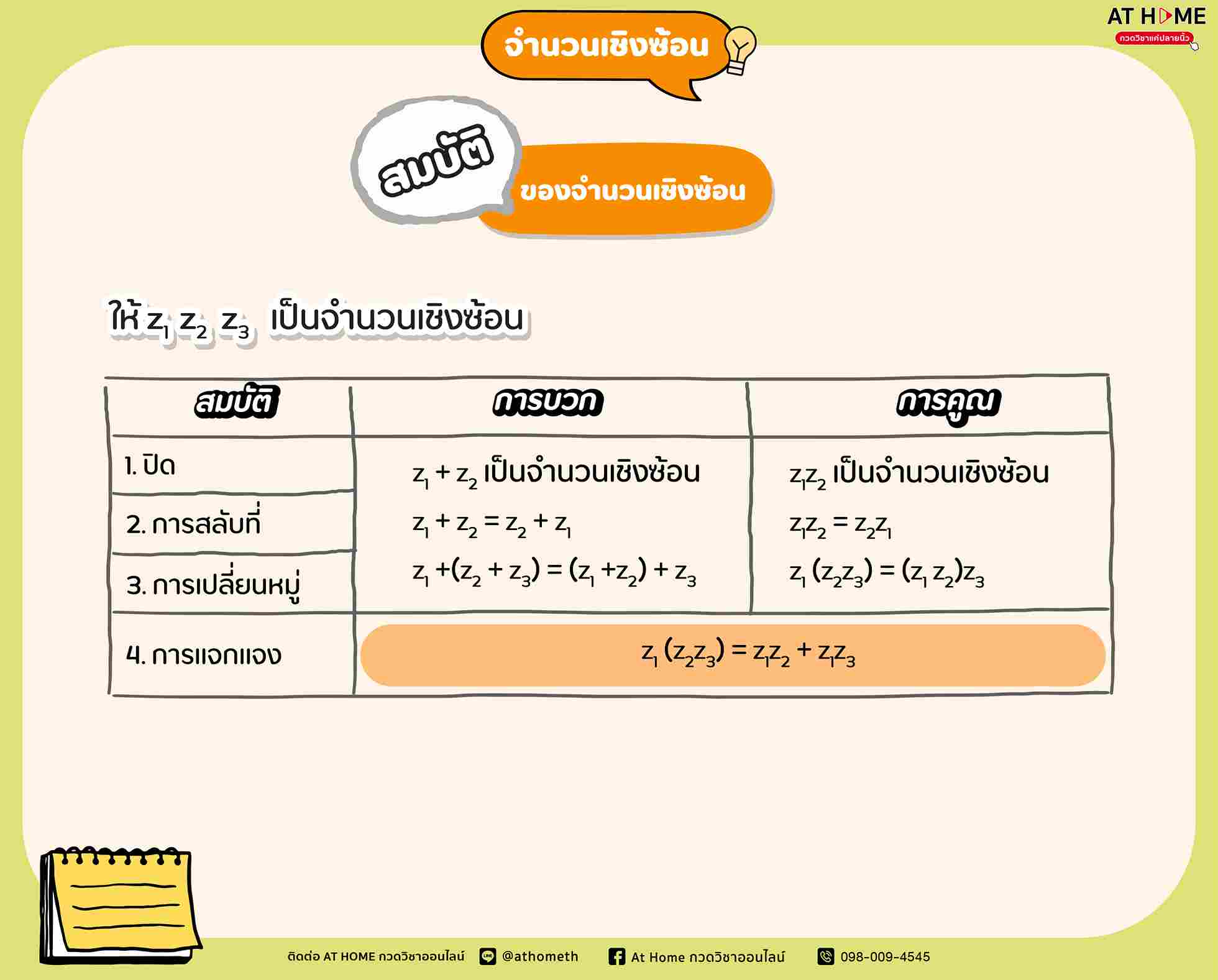
สมบัติของจำนวนเชิงซ้อน สรุป

---

สังยุคของจำนวนเชิงซ้อน

---

การหารจำนวนเชิงซ้อน

---

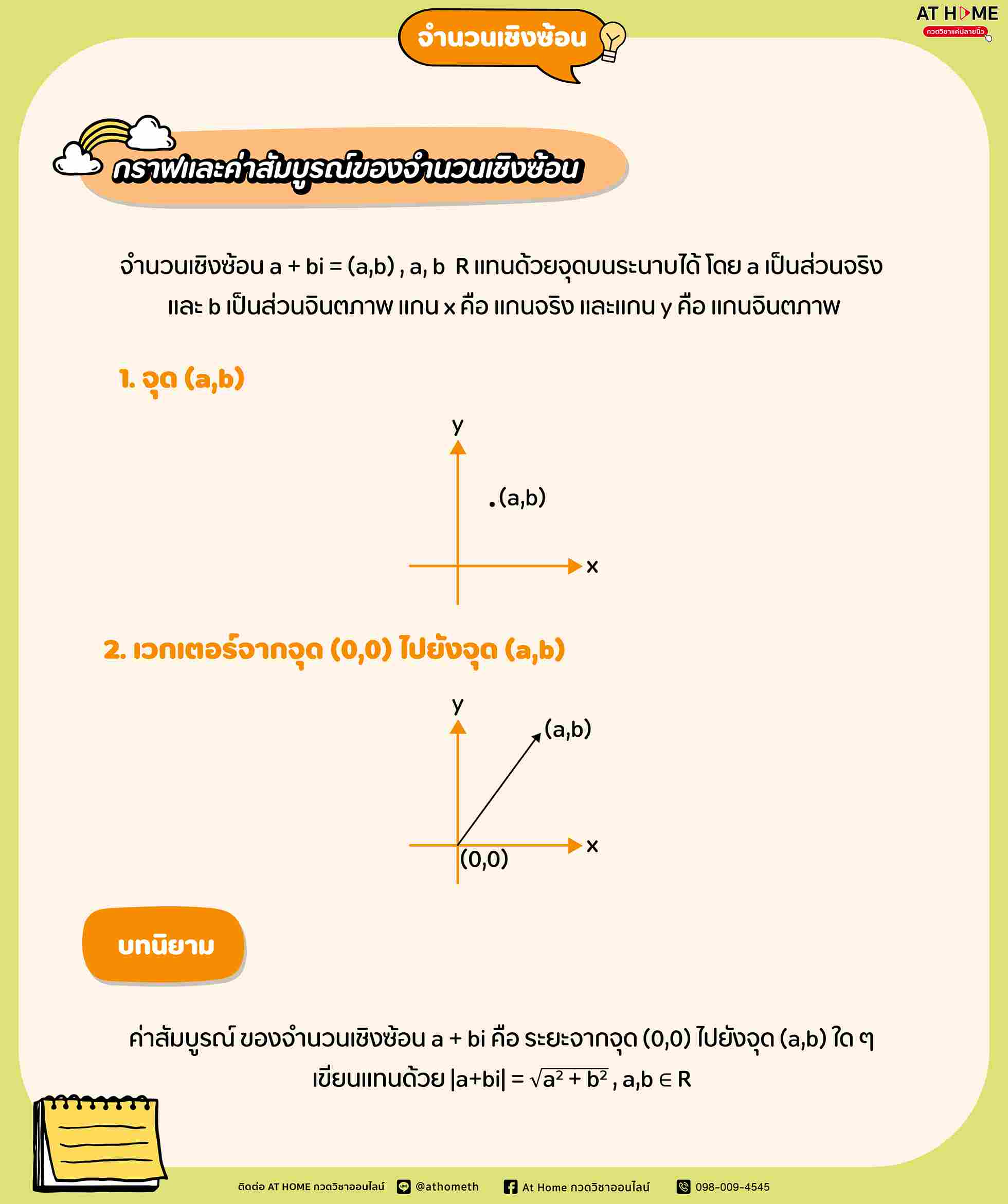
กราฟและค่าสัมบูรณ์ของจำนวนเชิงซ้อน

---

สมบัติของค่าสัมบูรณ์

---

บทประยุกต์ของค่าสัมบูรณ์ในเชิงกราฟ

---

รากที่ 2 ของจำนวนเชิงซ้อน

---

จำนวนเชิงซ้อนในรูปเชิงขั้ว

---

ทฤษฎีบทของเดอมัวร์

---

รากที่ n ของจำนวนเชิงซ้อน

---

สมการพหุนาม

ถ้า p(x) = a_nxⁿ + a_n-1 x^n-1  + a_n-2 x ^n-2 + ….+ a₁x + a₀
โดยที่ n เป็นจำนวนเต็มบวกและ a_n , a_n-1 , a_n-2 , ….. a₁, a₀ เป็นจำนวนจริงที่ a_n 0
แล้ว p(x) จะเป็นพหุนามดีกรี n (n มากกว่าหรือเท่ากับ 1)

ทฤษฎีบทหลักมูลของพีชคณิต 

ถ้า P(x) = 0 เป็นสมหารพหุนามดีกรี n (n มากกว่าหรือเท่ากับ1) แล้ว จะมีคำตอบที่เป็นจำนวนเชิงซ้อนอย่างน้อยหนึ่งคำตอบ

ทฤษฎีบท

ถ้า P(x) = 0 เป็นสมหารพหุนามดีกรี n (n มากกว่าหรือเท่ากับ 1) แล้ว จะมีคำตอบทั้งหมด n คำตอบ
(คำตอบอาจซ้ำกันได้)

ทฤษฎีบท

ถ้า P(x) = 0 เป็นสมหารพหุนามดีกรี n (n มากกว่าหรือเท่ากับ 1) และ z เป็นจำนวนเชิงซ้อนที่เป็นคำตอบของสมการ
แล้ว z จะเป็นคำตอบของสมการด้วย

---

คำถามที่พบบ่อย (FAQ)

---