วงกลม เป็นรูปเรขาคณิตสองมิติอย่างหนึ่งที่มีสมบัติและความสัมพันธ์กันที่น่าสนใจมากระหว่างองค์ประกอบภายในทั้งหมดนั้น แน่นอนว่าเป็นเรื่องใหม่ที่น้องม.3 ต้องทำความเข้าใจ แต่ไม่ต้องกังวลไปน้า เพราะพี่ ๆ ATHOME ได้รวบรวมเอาข้อสอบพร้อมเฉลยดี ๆ มาให้น้อง ๆ ได้ฝึกทำกันแล้วนะคะ
ส่วนต่าง ๆ ของวงกลม
( รอใส่รูปภาพ 1 )
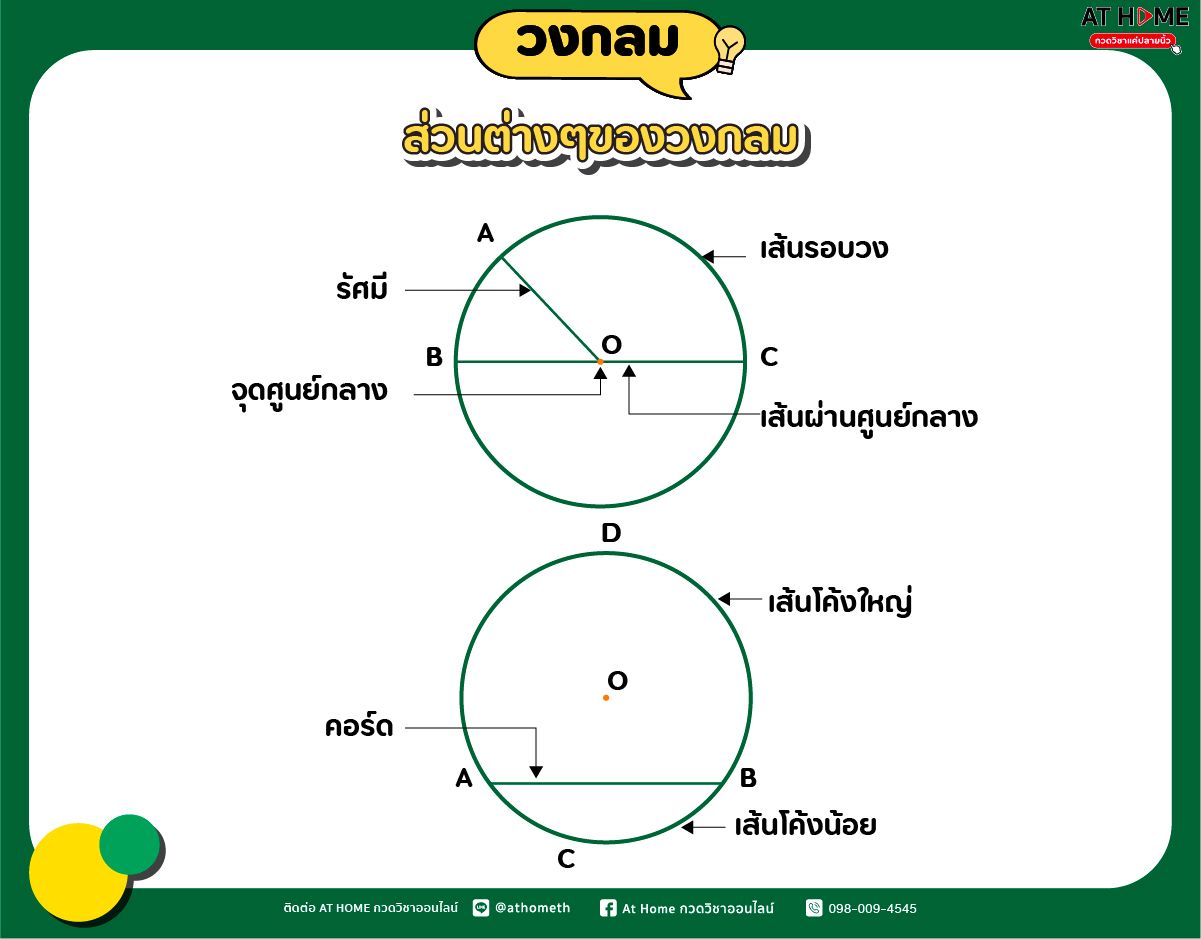
การเรียกชื่อวงกลมวงหนึ่งที่มีจุดศูนย์กลางตามที่กาหนดให้ อาจเรียกตามชื่อของจุดศูนย์กลาง ของวงกลมนั้น เช่น วงกลมที่มีจุด O เป็นจุดศูนย์กลาง อาจเรียกว่า วงกลม O
รัศมีของวงกลม หมายถึง ระยะระหว่างจุดศูนย์กลางของวงกลมและจุดบนวงกลม หรือ หมายถึง ส่วนของเส้นตรงที่มีจุดศูนย์กลางและจุดบนวงกลมเป็นจุดปลาย
วงกลมวงหนึ่งมีรัศมีเป็นจานวนมากมายนับไม่ถ้วน และรัศมีของวงกลมเดียวกันจะยาวเท่ากันทุกเส้น
วงกลมสองวงท่ีมีรัศมียาวเท่ากัน สามารถขยับให้วงกลมสองวงน้ันทับกันได้สนิท
สามารถกล่าวได้ว่า ” กลมสองวงที่มีรัศมียาวเท่ากันทุกประการ “
นอกจากส่วนประกอบต่าง ๆ ของวงกลมที่กล่าวมาแล้วนั้น ยังมีส่วนอื่น ๆ ที่มีความสำคัญมาก ไม่ว่าจะเป็น คอร์ด เส้นตัดวงกลม และเส้นสัมผัสวงกลม
คอร์ด คือ ส่วนของเส้นตรงที่มีจุดปลายทั้งสองอยู่บนวงกลมเดียวกัน คอร์ดแต่ละเส้นจะแบ่ง วงกลมออกเป็นส่วนโค้งสองส่วนโค้ง
ครึ่งวงกลม คือ เส้นผ่านศูนย์กลางของวงกลมที่มีคอร์ดยาวที่สุดซึ่งแบ่งวงกลมออกเป็นส่วนของเส้นโค้งสองส่วนที่เท่ากันทุกประการ
ทฤษฎีเกี่ยวกับมุมที่จุดศูนย์กลางและมุมในส่วนของวงกลม
| ทฤษฎีบท มุมในครึ่งวงกลมมีขนาด 90 องศา หรือหนึ่งมุมฉาก |
| ทฤษฎีบท (มุมที่จุดศูนย์กลาง) มุมที่จุดศูนย์กลางของวงกลมจะมีขนาดเป็นสองเท่าของขนาดของมุมในส่วนโค้งของวงกลมที่รองรับด้วยส่วนโค้งเดียวกัน |
| ทฤษฎีบท ในวงกลมเดียวกัน มุมในส่วนโค้งของวงกลมที่รองรับด้วยส่วนโ๕้งเดียวกันจะมีขนาดเท่ากัน |
| ทฤษฎีบท ในวงกลมที่เท่ากันทุกประการหรือในวงกลมวงเดียวกัน ถ้ามุมที่จุดศูนย์กลางมีขนาดเท่ากัน แล้วส่วนโค้งที่รองรับมุมที่จุดศูนย์กลางนั้นยาวเท่ากัน |
| ทฤษฎีบท (มุมในส่วนโค้งของวงกลม-ส่วนโค้งที่รองรับมุมนั้น) ในวงกลมที่เท่ากันทุกประการหรือในวงกลมวงเดียวกัน ถ้ามุมในส่วนโค้งของวงกลมนั้นมีขนาดเท่ากัน แล้วส่วนโค้งที่รองรับมุมทั้งนั้นยาวเท่ากัน |
| ทฤษฎีบท ในวงกลมที่เท่ากันทุกประการหรือในวงกลมวงเดียวกัน ถ้าส่วนโค้งยาวเท่ากัน แล้วมุมที่จุดศูนย์กลางที่รองรับด้วยส่วนโค้งนั้นมีขนาดเท่ากัน |
| ทฤษฎีบท (ส่วนโค้งของวงกลมที่รองรับมุม-มุมในส่วนโค้งของวงกลม) ในวงกลมที่เท่ากันทุกประการหรือในวงกลมวงเดียวกัน ถ้าส่วนโค้งยาวเท่ากัน แล้วมุมในส่วนโค้งของวงกลมที่รองรับด้วยส่วนโค้งนั้นจะมีขนาดเท่ากัน |
ทฤษฎีบทวงกลมเกี่ยวกับคอร์ดวงกลม
| ทฤษฎีบท (ส่วนโค้งน้อย-ส่วนโค้งใหญ่) ในวงกลมที่เท่ากันทุกประการหรือในวงกลมวงเดียวกัน ถ้าคอร์ดสองคอร์ดยาวเท่ากัน แล้วคอร์ดทั้งสองจะตัดวงกลมทำให้ส่วนโค้งน้อยยาวเท่ากัน และส่วนโค้งยาวยาวเท่ากัน |
| ทฤษฎีบท (คอร์ด-ส่วนโค้งของวงกลม) ในวงกลมที่เท่ากันทุกประการหรือในวงกลมวงเดียวกัน ถ้าคอร์ดสองคอร์ดตัดวงกลมทำให้ส่วนโค้งน้อยยาวเท่ากัน และส่วนโค้งใหญ่ยาวเท่ากันแล้วคอร์ดทั้งสองคอร์ดนั้นจะยาวเท่ากัน |
| ทฤษฎีบท (คอร์ด-จุดศูนย์กลางของวงกลม) ส่วนของเส้นตรงซึ่งผ่านจุดศูนย์กลางของวงกลมและตัดคอร์ดที่ไม่ใช่เส้นผ่านศูนย์กลาง จะมีสมบัติดังนี้ 1. ถ้าส่วนของเส้นตรงตั้งฉากกับคอร์ด แล้วส่วนของเส้นตรงนั้นจะแบ่งครึ่งคอร์ด 2.ถ้าส่วนของเส้นตรงแบ่งครึ่งคอร์ด แล้วส่วนของเส้นตรงนั้นจะตั้งฉากกับคอร์ด |
| ทฤษฎีบท (เส้นตรง-จุดศูนย์กลาง) เส้นตรงที่ตั้งฉากและแบ่งครึ่งคอร์ดของวงกลม จะผ่านจุดศูนย์กลางของวงกลมนั้น |
| ทฤษฎีบท มีวงกลมเพียง 1 วงเท่านั้นที่ผ่านจุด 3 จุด ที่ไม่อยู่บนเส้นตรงเดียวกัน |
| ทฤษฎีบท (รูปสี่เหลี่ยมแนบในวงกลม) ถ้ารูปสี่เหลี่ยมใด ๆ มีผลบวกของขนาดของมุมตรงข้ามเท่ากับสองมุมฉาก แล้วรูปสี่เหลี่ยมนั้นแนบในวงกลมได้ |
| ทฤษฎีบท (คอร์ด-จุดศูนย์กลาง) 1.ในวงกลมวงหนึ่ง ถ้าคอร์ดสองเส้นยาวเท่ากัน แล้วคอร์ดทั้งสองนั้นจะอยู่ห่างจากจุดศูนย์กลางของวงกลมเป็นระยะเท่ากัน 2.ในวงกลมวงหนึ่ง ถ้าคอร์ดสองเส้นอยู่ห่างจากจุดศูนย์กลางของวงกลมเป็นระยะเท่ากัน แล้วคอร์ดทั้งสองนั้นจะยาวเท่ากัน |
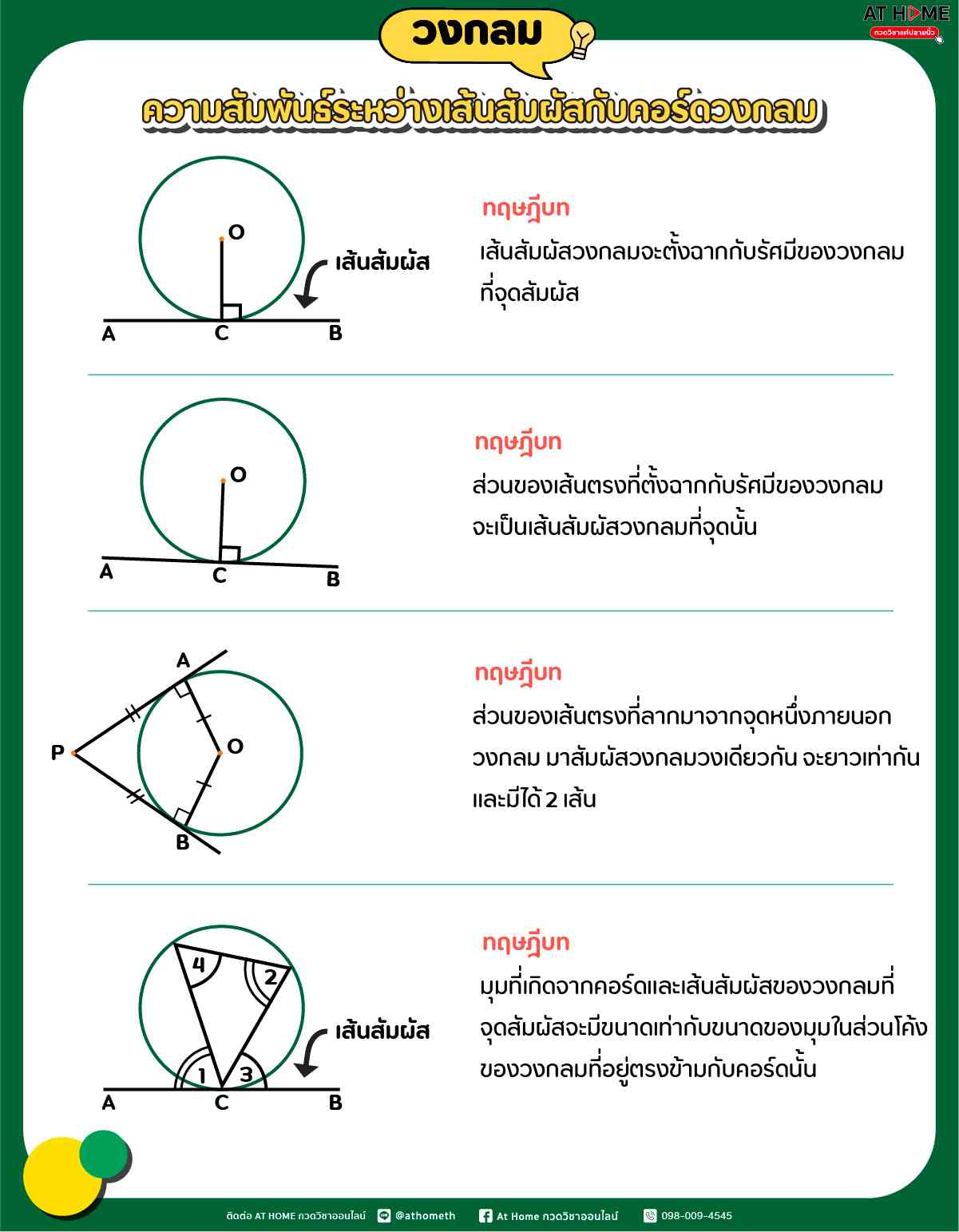
ทฤษฎีบทเกี่ยวกับเส้นสัมผัสวงกลม
| ทฤษฎีบท เส้นสัมผัสวงกลมจะต้องฉากกับรัศมีของวงกลมที่จุดสัมผัส |
| ทฤษฎีบท (บทกลับ) เส้นตรงที่ตั้งฉากกับรัศมีของวงกลมที่จุดจุดหนึ่งบนวงกลม จะเป็นเส้นสัมผัสวงกลมที่จุดนั้น |
| ทฤษฎีบท (จุดภายนอก-เส้นสัมผัส) ส่วนของเส้นตรงที่ลากมาจากจุดจุดหนึ่งภายนอกวงกลม มาสัมผัสวงกลมวงเดียวกัน จะยาวเท่ากันและมีได้สองเส้น |
| ทฤษฎีบท (คอร์ด-เส้นสัมผัส) มุมที่เกิดจากคอร์ดและเส้นสัมผัสของวงกลมที่จุดสัมผัส จะมีขนาดเท่ากับขนาดของมุมในส่วนโค้งของวงกลมที่อยู่ตรงข้ามกับคอร์ดนั้น |
ความสัมพันธ์ระหว่างเส้นสัมผัสกับคอร์ดวงกลม
โจทย์มุมที่จุดศูนย์กลางและมุมในส่วนโค้งของวงกลม
ทฤษฎีบทที่สำคัญเกี่ยวกับวงกลม
โจทย์ 1 จงเขียนรูปแสดงมุมที่จุดศูนย์กลาง-มุมในส่วนโค้งของวงกลม
วิธีทำ มุมที่จุดศูนย์กลาง
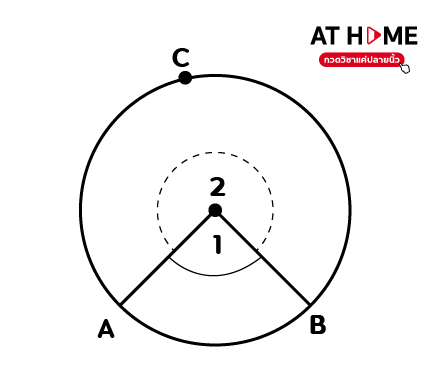
มุม 1 เป็นมุมที่จุดศูนย์กลางของวงกลมรองรับด้วยส่วนโค้ง AB
มุม 2 เป็นมุมที่จุดศูนย์กลางของวงกลมรองรับด้วยส่วนโค้ง ACB
มุมในส่วนโค้งของวงกลม
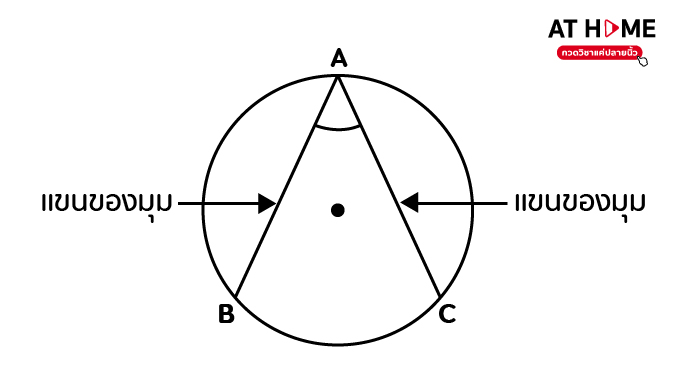
มุม A เป็นมุมในส่วนโค้งของวงกลมที่รองรับด้วยส่วนโค้ง BC
โจทย์มุมในครึ่งวงกลม
- ให้ AB เป็นเส้นผ่านศูนย์กลางวงกลม O และมุม BAC = 70 องศา จงหามุม ABC
วิธีทำ
เนื่องจากมุม ACB = 90 องศา เพราะมุมในครึ่งวงกลม
มุม A + มุม B + มุม C = 180 องศา เพราะมุมภายในสามเหลี่ยม
เท่ากับ 70 + มุม B + 90 = 180 องศา
มุม B = 180 – 70 – 90 = 20 องศา คือมุม ABC
โจทย์เรื่องคอร์ดวงกลม
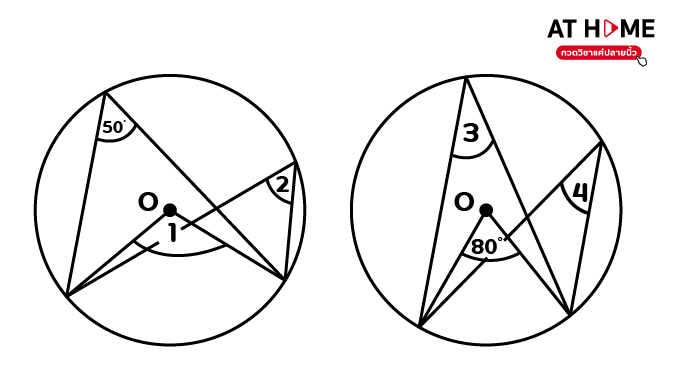
- จากภาพ ให้ O เป็นจุดศูนย์กลางวงกลม จงหา 1. มุม 1 2. มุม 2 3. มุม 3 4. มุม 4
วิธีทำ
จากรูปซ้ายมือ
1. มุม 1 = 2(50) = 100 องศา
2.มุม 2 = 50 องศา
จากรูปขวามือ
1. มุม 3 = ครึ่งหนึ่งของมุม 80 องศา = ½ (80) = 40 องศา
2. มุม 4 = ครึ่งหนึ่งของมุม 80 องศา = ½ (80) = 40 องศา
2. จากรูปต่อไปนี้จงหา 1. ขนาดของมุม 1 2. ขนาดของมุม 2
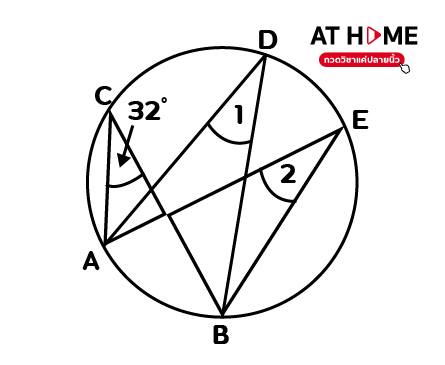
วิธีทำ จากรูปจะพบว่ามุม 32 องศา อยู่บนเส้นโค้ง AB ซึ่งมุม 1 และมุม 2 ก็เช่นกัน จะได้ว่า
- มุม 1 = 32 องศา 2. มุม 2 = 32 องศา
ตอบ 1. 32 องศา 2. 32 องศา
3. ให้ O เป็นจุดศูนย์กลางวงกลม จงหาค่ามุม
- มุม x 2. มุม y
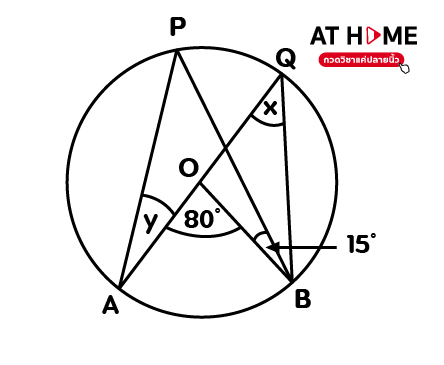
วิธีทำ เราเขียนมุม u เพิ่มเข้าในไปรูป
ใช้หลักมุมที่จุดศูนย์กลาง
- มุม AOB = 2(มุมx) (มุมศูนย์กลางเป็น 2 เท่าของมุมที่เส้นรอบวง)
มุม x = 80/2 = 40 องศา
มุม u = มุม x = 40 องศา มุมที่ฐานของสามเหลี่ยมหน้าจั่ว
- มุม PAQ = มุม PBQ (มุมในส่วนของวงกลมเดียวกัน)
มุม y = มุม u – 15 องศา
มุม y = 40 – 15 = 25 องศา
ตอบ 1. มุม x = 40 องศา 2. มุม y = 25 องศา
โจทย์เส้นตัดวงกลม
- จงหาขนาดของ x จากรูป
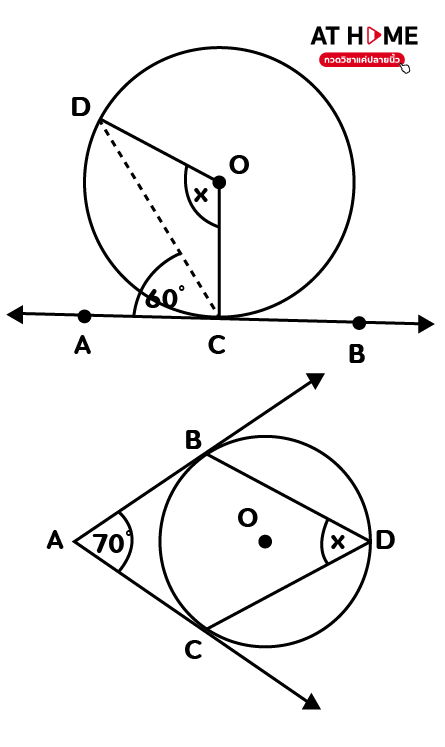
วิธีทำ 1. 60 องศา + มุม DCO = 90 องศา เพราะเส้นสัมผัส AB ตั้งฉากกับรัศมี OC
มุม DCO = 90 องศา – 60 องศา = 30 องศา
แต่สามเหลี่ยม ODC เป็นสามเหลี่ยมหน้าจั่ว เพราะ รัศมี DO = รัศมี OC
จะได้ มุม ODC = DCO เพราะมุมของสามเหลี่ยมหน้าจั่ว
= 30 องศา
ดังนั้น มุม DOC = 180 – 30 – 30 เพราะมุมในสามเหลี่ยม, มุม DOC = 120 องศา (=มุม x)
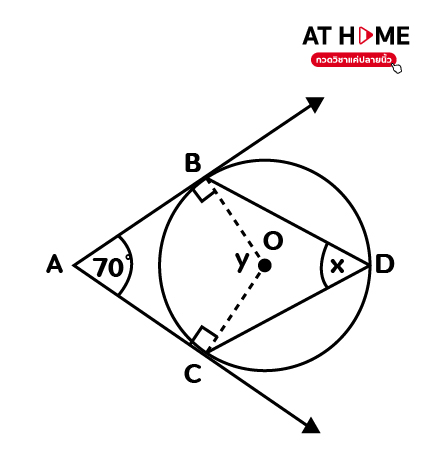
- หา y จากในรูปสี่เหลี่ยม ABOC ได้ มุม A + มุม ABO + มุม y + มุม ACO = 360 องศา
จะได้ 70 + 90 + มุม y + 90 = 360
มุม y = 360 – 70 – 90 – 90 = 110 องศา
หามุมที่เส้นรอบวง คือ หามุม x
มุมที่จุดศูนย์กลาง (คือ มุม y) = 2 เท่าของมุมที่เส้นรอบวง
จะได้ มุม y = 2 มุม x
110 องศา = 2 มุม x
มุม x = 110/2 = 55 องศา
ตอบ 1. มุม x = 120 องศา 2. มุม x = 55 องศา
เฉลย แบบฝึกหัด วงกลม แบบฝึกหัดแบบละเอียด
- จากรูปที่กำหนดให้ต่อไปนี้ จงหาค่า x และ y โดยกำหนดให้ O เป็นศูนย์กลางของวงกลม
วิธีทำ y = 90 องศา เป็นมุมภายในครึ่งวงกลม
y + x + 40 = 180 องศา มุมภายในของรูปสามเหลี่ยมรวมกันได้ 180 องศา
x = 180 – 90 – 40
ดังนั้น x = 50 องศา และ y = 90 องศา
- จากรูป ส่วนของเส้นตรง AB เป็นเส้นผ่านศูนย์กลางของวงกลม O และมุม BAC = 65 องศา จงหาขนาดของมุม ABC
วิธีทำ มุม ACB = 90 องศา เป็นมุมในครึ่งวงกลม
มุม CAB + ABC + BCA = 180 องศา มุมภายในของรูปสามเหลี่ยมรวมกันได้ 180 องศา
มุม ABC = 180 – 65 = 115 องศา
ตอบ มุม ABC เท่ากับ 115 องศา
- จากรูปส่วนของเส้นตรง AB เป็นเส้นผ่านศูนย์กลางของวงกลม CD ตั้งฉากกับ AB และมุม BAC = 37 องศา จงหาขนาดของมุม BCD
วิธีทำ มุม ACB = 90 องศา เป็นมุมในครึ่งวงกลม
มุม BAC = 37 องศา กำหนดให้
มุม ACB + มุม BAC + มุม ABC = 180 องศา (มุมภายในรูปสามเหลี่ยมเท่ากับ 180 องศา)
มุม ABC = 53 องศา
มุม OCB + มุม BOC + มุม CBO = 180 องศา (มุมภายในรูปสามเหลี่ยมเท่ากับ 180 องศา)
มุม OCB = 37 องศา
มุม BCD = มุม OBC = 37 องศา
ดังนั้น มุม BCD = 37 องศา
แบบฝึกหัดเรื่อง วงกลม โจทย์ หาค่าตัวแปรภายในวงกลม
| 4. |
| 5. |
| 6. |
| 7. |
| 8. |
| 9. |
| 10. |
คำถามที่พบบ่อย (FAQ)
มุมในครึ่งวงกลมมีขนาดกี่องศา
มุมในครึ่งวงกลมเท่ากับ 180 องศา
รัศมีวงกลม สูตร
สูตรเส้นรอบรูปวงกลม = 2r สูตรพื้นที่วงกลม = r2 ( รอใส่พายอาร์ )
ในวงกลมหนึ่งวง มีคอร์ดทั้งหมดกี่เส้น
ในหนึ่งวงกลมสามารถมีจำนวนคอร์ดได้นับไม่ถ้วน
รัศมีของวงกลม เป็นเส้นตัดวงกลม หรือไม่ เพราะเหตุใด
รัศมีวงกลมไม่จัดเป็นเส้นตัดของวงกลม เนื่องจากเส้นตัดของวงกลมนั้นจะต้องตัดวงกลมสองจุด ส่วนรัศมีวงกลมคือเส้นที่อยู่ห่างจากจุดศูนย์กลงไปยังจุดใด ๆ บนเส้นรอบวง
รัศมีวงกลมมีกี่เส้น
มากมายนับไม่ถ้วน
จำนวนเส้นตัดวงกลมในวงกลมหนึ่งวงมีจำนวนทั้งหมดกี่เส้น
มีจำนวนมากมายนับไม่ถ้วน
เส้นตัดวงกลมสามารถตัดผ่านจุดศูนย์กลางได้หรือไม่
เส้นตัดวงกลมสามารถตัดผ่านจุดศูนย์กลางของวงกลมได้
ในวงกลมหนึ่งวงสามารถมีเส้นสัมผัสได้ทั้งหมดกี่เส้น
วงกลมหนึ่งวงมีเส้นสัมผัสได้จำนวนมากมายนับไม่ถ้วน
เส้นสัมผัสวงกลมสามารถผ่านจุดศูนย์กลางได้หรือไม่
เส้นสัมผัสวงกลมผ่านจุดศูนย์กลางไม่ได้
บทเรียนเรื่องวงกลม ม. 3 ก็ประกอบไปด้วยสาระคร่าว ๆ ประมาณนี้เลยนะคะ ถ้าน้อง ๆ คนไหนรู้สึกสนใจและอยากให้พี่ ๆ นำเสนอสาระย่อยง่าย อ่านแล้วจำดี สามารถนำไปใช้ในห้องสอบได้ทันทีแบบนี้อีก ก็อย่าลืมคอยติดตามความเคลื่อนไหวของเว็บไซต์ ATHOME แพลตฟอร์มกวดวิชาออนไลน์ที่คอยมอบความรู้ในสาระวิชาต่าง ๆ ครบถ้วน และละเอียด เข้าใจง่ายแบบนี้เรื่อย ๆ เลยน้า





